Registrazione gratuita per l’accesso al sito
I recenti attentati in varie città europee hanno mostrato la necessità di studiare il comportamento delle folle in condizioni di emergenza. In Italia a seguito dei gravi fatti accaduti a Torino il 3 giugno 2017, quando in occasione della finale di Champions League, tra Juventus e Real Madrid, in piazza S. Carlo dove fu installato un maxischermo per permettere ai tifosi di seguire in diretta la partita che si disputava a Cardiff, a seguito del comportamento di un gruppo di rapinatori che utilizzavano spray urticante per aprirsi la strada, dopo aver rubato oggetti di valore tra il pubblico, si è scatenato il panico. Le persone presenti hanno creato una calca per fuggire, che ha provocato un totale di 1527 feriti e la morte per schiacciamento di una donna.
Questi fatti hanno portato a nuove considerazioni e riflessioni sulla sicurezza degli eventi di pubblico spettacolo e in modo più in generale sugli eventi pubblici in genere, non più intesi come insieme di misure di prevenzione e protezione da adottare per mitigare il rischio dovuto alla casualità, ma anche come insieme di misure tese a prevenire e minimizzare gli impatti di azioni criminose.
L’attenzione degli esperti era tutta dedicata agli aspetti di “Safety” intesa come il complesso di disposizioni, sia cogenti che dettate dall’esperienza, volte a tutelare l’integrità fisica delle persone da eventi accidentali che possono compromettere il funzionamento delle strutture realizzate per le manifestazioni. Oggi per la progettazione e gestione di questi eventi si deve prestare particolare attenzione anche agli aspetti di “Security” intesa come il complesso di misure atte a garantire l’ordine e la sicurezza dei cittadini, da comportamenti umani (dolosi e/o colposi) che possono turbare l’ordine pubblico e la sicurezza delle persone.
Queste riflessioni hanno portato alla pubblicazione di una serie di circolari da parte del Ministero dell’Interno relative, sia il settore della Safety che il settore della Security (consultabili al seguente link), che nell’arco di circa un anno hanno completamente rivoluzionato il modo di approcciare l’argomento, sia da parte degli organizzatori degli eventi che da parte degli organi di controllo.
La conferenza Stato-Regioni il 5 Agosto 2014, ha approvato le “Linee di indirizzo sull’organizzazione dei soccorsi sanitari negli eventi e nelle manifestazioni programmate”. Nelle linee guida è previsto un modello speditivo per quantificare i rischi di eventi con grande affluenza di pubblico e predisporre le risorse adeguate per il soccorso sanitario, conosciuto come “algoritmo di Maurer” (fogli di calcolo per l’applicazione del metodo 1, 2).
Il Ministero dell’Interno con una Circolare del 28 luglio 2017– “Modelli organizzativi per garantire alti livelli di sicurezza in occasione di manifestazioni pubbliche. Direttiva.” ha disposto l’utilizzo dello stesso metodo, attualizzando alcuni parametri relative alle esigenze di Safety, rispetto al soccorso sanitario, per la gestione delle Pubbliche Manifestazioni, con riferimento all’accordo Stato-Regioni del 5 Agosto 2014.
Esodo
Riveste particolare importanza, in occasione di manifestazioni pubbliche organizzate in luoghi all’aperto, l’esame delle condizioni relative all’esodo delle persone presenti, effettuando una attenta pianificazione in ragione degli affollamenti massimi previsti e sostenibili, alle le modalità di afflusso e deflusso, alla presenza di ostacoli, alla disponibilità di spazi liberi da assimilare a luogo sicuro statico o dinamico ovvero temporaneo o permanente.
A tal fine, gli strumenti di modellazione fluido-dinamica e di simulazione del comportamento umano in emergenza, da utilizzare nell’ambito dell’approccio ingegneristico alla sicurezza antincendio, per valutare ii livello di rischio e progettare le conseguenti misure compensative, costituiscono un utile supporto, sia per gli organizzatori e i gestori degli eventi che per gli organi di controllo (Commissioni di Vigilanza sui Locali di pubblico spettacolo, Comitato provinciale per l’ordine e la sicurezza pubblica).
Lo scopo delle si simulazioni d’esodo mediante modelli “agent based” è quello di supportare la progettazione del sistema di gestione della sicurezza attraverso la visualizzazione 3D di ciò che potrebbe accadere durante l’evacuazione in varie configurazioni al variare di:
- affollamento;
- la disposizione degli utenti mediante la suddivisione in settori
- il posizionamento delle vie di esodo
- il comportamento degli agenti che effettuano l’evacuazione (comportamento sociale)
L’applicazione dei metodi propri della FSE è prevista dalla Circolare del Ministero dell’Interno del 18 luglio 2018 “Linea guida per l’individuazione delle misure di contenimento del rischio in manifestazioni pubbliche con peculiari condizioni di criticità” che dispone:
“……….. Per le manifestazioni storiche caratterizzate da peculiari criticità e per le quali le condizioni di tutela dei beni storici, monumentali ed ambientali non consentano la completa attuazione delle misure riportate nella presente linea guida potrà farsi ricorso, ai fini del calcolo dei parametri dell’affollamento e dell’esodo, ai metodi prestazionali previsti dagli strumenti propri dell’ingegneria della sicurezza. A tal proposito, adottando l’approccio ingegneristico, il progettista dovrà dettagliare i passaggi che conducono ad individuare le condizioni più rappresentative del rischio al quale l’attività è esposta e quali siano i livelli di prestazione cui riferirsi in relazione agli obiettivi di sicurezza da perseguire. In funzione degli obiettivi di sicurezza individuati, il progettista dovrà indicare quali sono i parametri significativi presi a riferimento per garantire il raggiungimento degli stessi obiettivi. Pertanto, dovranno essere quantificati i livelli di prestazione, intendendo con ciò l’individuazione di valori di riferimento rispetto ai quali verificare che le scelte progettuali in termini di misure di sicurezza adottate consentano di perseguire i risultati attesi. Tali valori potranno essere desunti dalla specifica letteratura tecnica riconosciuta a livello nazionale ed internazionale. Infine, in esito ai risultati dell’elaborazione effettuata, essi costituiranno i parametri di riferimento per attestare il raggiungimento dei livelli di prestazione prefissati e validare la progettazione proposta.”
L’approccio prestazionale non si occupa di verificare il rispetto di una norma o di una probabilità di accadimento, il progettista definisce lo scopo del progetto e l’obiettivo da conseguire ed effettua la verifica sulla rispondenza dei requisiti stabiliti; si effettua quindi una valutazione quantitativa del livello di sicurezza. Nel caso dell’evacuazione si accerta che il tempo disponibile per l’evacuazione (ASET-Available Safe Egress Time) è compatibile, a meno di un fattore di sicurezza, con il tempo disponibile per l’evacuazione (RSET-Request Safe Egress Time).
Con il metodo prestazionale per ogni caso studiato è possibile prevedere il comportamento dell’evento (incendio/evacuazione, ecc.) e di tutte le variabili ad esso associate, in questo modo si realizza una progettazione che risulta su misura e che permette di definire in modo più preciso le misure di sicurezza da adottare. Nel caso trattato, della evacuazione di grandi aree all’aperto, è possibile determinare l’influenza del singolo percorso di esodo sul movimento di grandi folle al fine di minimizzare i tempi di evacuazione e di eliminare qualunque ostacolo che l’ambiente stesso possa aggiungere alle condizioni di evacuazione.
Utilizzando l’approccio prestazionale, il progettista attribuisce alle misure gestionali (formazione, addestramento, gestione dell’emergenza, sorveglianza, ecc.) un ruolo pari alle misure di prevenzione e protezione classiche, conferendo alle medesime una funzione strategica nel contesto della progettazione.
Gli strumenti della FSE
Si vuole in questo contesto fornire indicazioni utili relative alla teoria utilizzata per la determinazione della velocità di percorrenza utilizzata in alcuni modelli di calcolo concernenti l’evacuazione.
Nel “SFPE handbook of fire protect Engineering” è riportata la teoria di Fruin, Pauls, Predtechenskii e Milinskii che hanno effettuato più esperimenti rilevando che la velocità di movimento degli individui in gruppo o facenti parte di un gruppo in evacuazione, è una funzione della densità di affollamento. (“numero massimo di occupanti assunto per unità di superficie lorda dell’ambito di riferimento (persone/m2)”. G.1.9 Codice Prevenzione Incendi – D.M. 3/8/2015)
Se la densità di affollamento è inferiore a circa 0,05 persone/ft2 (0,54 persone/m2) nel percorso di uscita, gli individui si muoveranno al loro ritmo, indipendentemente dalla velocità degli altri. Se la densità di affollamento supera circa 0,35 persone/ft2 (3,8 persone/m2), si presume che non si verificherà nessun movimento fino a quando non si sarà ridotto il ridurre il numero delle persone. Tra i limiti di densità di affollamento di 0,05 e 0,35 persone/ft2 (0,54 e 3,8 persone/m2), si presume che la relazione tra velocità e densità di affollamento sia rappresentata da una funzione lineare. L’equazione della funzione è la seguente:
S = k – a k D
dove:
S = Velocità in piano
D = densità delle persone per mq (densità di affollamento)
a = costante assume il valore di 2.86 ft/min con densità di affollamento in persone/ft2
a = costante assume il valore di 0.266 m/sec con densità di affollamento in persone/m2
k assume i seguenti valori:
k1 =persone/ft2 ;
k2 = persone/m2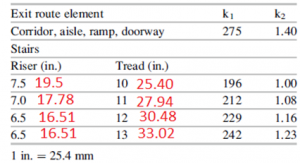
Nelle scale la velocità di percorrenza è funzione delle dimensioni del gradino, alzata (Riser) e pedata (Tread). In rosso sono riportati i valori alzata e pedata in cm.
La velocità di evacuazione delle scale varia approssimativamente come la radice quadrata del rapporto tra larghezza e l’altezza del gradino. Non ci sono dati sufficienti per valutare la probabilità che questa relazione resti al di fuori di questo intervallo.
La funzione è esplicitata nella seguente figura con la densità di affollamento in persone/ft2 e la velocità in ft/min.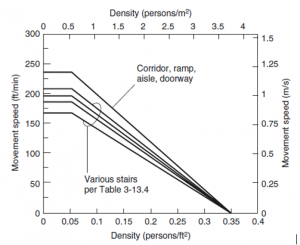
N.B. La tabella 3-13.4 citata nel grafico è da intendere la tabella prima riportata.
Come si può vedere nella figura la densità di affollamento massima può essere di 3.76 persone/m2. Al di sopra di questo limite, il movimento delle persone è fortemente condizionato.
La velocità massima possibile senza impedimenti si ottiene quando la densità di affollamento è inferiore a 0,05 persone/ft2 (0,54 persone/ m2). Queste velocità massime sono elencate nella seguente tabella: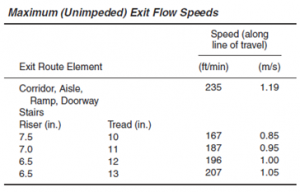
Conservativamente si assume che gli agenti non aumentano la velocità quando attraversano un pianerottolo tra due rampe di scale ma continuano a procedere alla stessa velocità ridotta associata al movimento delle scale.
Sebbene, in realtà, si possano raggiungere densità di popolazione superiori a 0,175 persone/ft2 (1,9 persone/m2), è prudente non utilizzare tali densità in un progetto ingegneristico di esodo. Questa densità di affollamento produce il maggiore movimento possibile; oltre questa densità, la portata delle persone diminuisce rapidamente. Se la densità di affollamento aumenta significativamente oltre 0,37 persone/ft2 (4 persone/m2), si potrebbero sviluppare condizioni di schiacciamento.
Valori simili di densità di affollamento sono previsti da NFPA 101 “Life Safety Code”, in questo caso i valori suggeriti sono da 0,142 persone/ft2 (1,54 persone/m2) a 0,003 persone/ft2 (0,022 persone/m2) a seconda del tipo di attività considerata (1 ft2 = 10.764 m2)
La massima densità di affollamento di progetto utilizzata in Italia è di 2 persone/m2, è prevista dalla Circolare del Ministero dell’Interno del 18 luglio 2018. Questa densità di affollamento viene applicata per determinare la capienza massima dei luoghi dove si svolgono manifestazioni pubbliche in aeree delimitate come una piazza.
Il codice di prevenzione incendi di cui al D.M. 3 agosto 2015 prevede una densità di affollamento massima uguale a 1.2 persone/m2.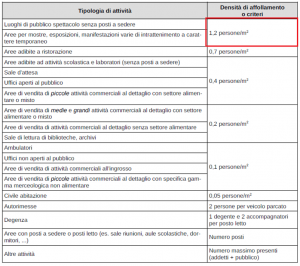
Tabella S.4-6 del D.M. 3 agosto 2015: Affollamento specifico o criteri per tipologia di attività
Analogo valore è previsto dal D.M. 19/agosto/1996, norma prescrittiva che disciplina le misure di prevenzione incendi per i locali di pubblico spettacolo, esclusivamente per sale da ballo e le discoteche.
Inoltre, la nota del Ministero dell’Interno prot. 10786 del 13/07/2010 fornisce indicazioni in merito alla densità di affollamento in strutture polifunzionali adibite occasionalmente ad attività di trattenimento, stabilisce che in caso di utilizzo di impianti sportivi per manifestazioni occasionali a carattere non sportivo, la sistemazione del pubblico in piedi nell’area destinata all’attività sportiva è consentita fino ad un massimo di 20 spettatori ogni 10 m2 di superficie all’uopo destinata (densità di affollamento uguale a 2 persone/m2).
Unica eccezione è costituita dal D.M. 18 marzo 1996 “Norme di sicurezza per la costruzione e l’esercizio degli impianti sportivi”, che all’art. 6, relativamente allo spazio riservato agli spettatori, indica:
” ….. La capienza dello spazio riservato agli spettatori è data dalla somma dei posti a sedere e dei posti in piedi; il numero dei posti in piedi si calcola in ragione di 35 spettatori ogni 10 metri quadrati di superficie all’uopo destinata“.
Ammettendo quindi una densità di affollamento di 3.5 persone/mq.
La norma poi aggiunge:
“…. sono ammessi posti in piedi negli impianti al chiuso con capienza fino a 500 spettatori ed in quelli all’aperto con capienza fino a 2.000 spettatori.”
Quindi in definitiva, densità di affollamento così alte sono ammesse esclusivamente in piccoli impianti sportivi.
Comportamento dei modelli di evacuazione in funzione della densità di affollamento
Il modello FDS + EVAC
FDS+EVAC simula realisticamente il fenomeno del rallentamento degli agenti dovuto alla congestione, il modello di simulazione considera le forze fisiche che si generano tra la folla e fra questa e l’ambiente esterno nelle varie situazioni. Queste forze includono le forze di contatto tra i corpi, le forze d’attrito tra i vari agenti e le forze che si esercitano tra questi e le pareti degli edifici posti all’interno dell’ambiente di simulazione.
In FDS+EVAC, ogni agente intelligente è seguito da un’equazione del moto. Ogni agente in questo modo ha delle proprietà personali e può assumere proprie strategie di evacuazione.
Il modello a base dell’algoritmo di movimento implementato in FDS+EVAC è il modello di forza sociale di Helbing e al., con i cambiamenti introdotti da Langston e da Korhonen e al. per includere una migliore descrizione della forma del corpo umano e considerare i gradi di libertà dovuti alla rotazione.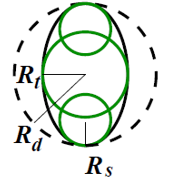
La forma del corpo umano è approssimata da una combinazione di tre cerchi sovrapposti. Rt, Rd e Rs rappresentano le variabili della dimensione del corpo.
Gli agenti predefiniti di FDS+EVAC presentano le caratteristiche mostrate dalla seguente tabella.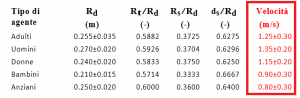
In particolare l’ultima colonna mostra la velocità di percorrenza senza impedimenti.
Le variabili che descrivono le dimensioni del corpo degli agenti sono Rd, Rt, Rs.
L’offset del cerchio che descrive le dimensioni degli agenti, introdotto per una descrizione più accurata del corpo mano per tenere conto della presenza delle spalle è dato da ds = Rd – Rs,
In FDS+EVAC ogni agente cerca di camminare con la propria specifica velocità verso un’uscita o verso qualche altro obiettivo prefissato, la velocità è variate in funzione delle forze sociali e di contatto che agiscono sull’agente stesso, inoltre contribuiscono al rallentamento gli effetti della densità del fumo e di alcuni elementi prodotti della combustione, tossici e asfissianti, come CO, CO2, CN, NOx, HCl, HBr, HF, SO2, NO2, C3H4O, CH2O.
Un agente a causa del fumo può ridurre la velocità di percorrenza fino a 1/10 della velocità iniziale fino a fermarsi a causa dell’incapacitazione dovuta alle sostanze tossiche ed irritanti. Le fiamme non hanno effetto sul movimento degli agenti.
Il seguente diagramma mostra come FDS+EVAC riduce la velocità di percorrenza in funzione della densità del fumo e quindi del coefficiente di estinzione: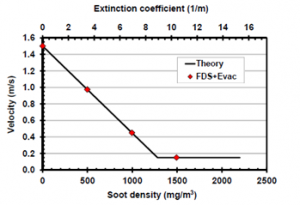
FDS+EVAC per adeguare la velocità di percorrenza degli agenti nella percorrenza delle scale (definite con il gruppo &STRS) e dei piani inclinati (definiti con il gruppo &EVSS) utilizza i parametri:
- FAC_V0_UP che rappresenta il fattore moltiplicativo della velocità di un agente in salita su un piano inclinato/scala (assume generalmente il valore di 0.4)
- FAC_V0_DOWN che rappresenta il fattore moltiplicativo della velocità di un agente in discesa su un piano inclinato/scala (assume generalmente il valore di 0.7)
- FAC_V0_HORI che rappresenta il fattore moltiplicativo della velocità di un agente in piano su un pianerottolo di un piano inclinato/scala (assume generalmente il valore di 1.0)
Il modello Pathfinder
Pathfinder utilizza la tecnica prima descritta tratta dal “SFPE handbook of fire protect Engineering”, in questo caso la velocità, 𝑣b alla quale un occupante si muove dipende da diversi fattori, tra cui la velocità massima dell’occupante (𝑣𝑚𝑎𝑥) specificata dall’utente, alla quale sono associati dei modificatori di velocità come in FDS+EVAC, in funzione del tipo di pavimento (in piano, rampa, scala) da percorrere, alla densità di affollamento degli occupanti all’interno dell’ambiente di simulazione
La velocità base degli agenti 𝑣b, è definita come:![]()
𝑣𝑚𝑎𝑥 è la velocità massima dell’agente così come definita dall’utente
𝑣𝑓(𝐷) è una frazione della velocità che dipende dalla densità di affollamento con le seguenti espressioni: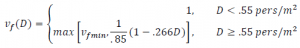
𝑣𝑓𝑚𝑖𝑛 è la frazione minima della velocità come definita nell’interfaccia utente (default = .15)
𝐷 è la densità di affollamento
𝑣𝑓𝑡 è una frazione di velocità che dipende dal tipo di pavimento che viene percorso dall’agente. È definita come: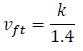
Per pavimento in piano e per rampe, k = 1,40 m/s. Per le scale, 𝑘 dipende dalle dimensioni, in termini di alzata e pedata dei gradini della scala.
Come abbiamo visto il SFPE handbook definisce 𝑘 per un insieme limitato di dimensioni dei gradini nel seguente modo: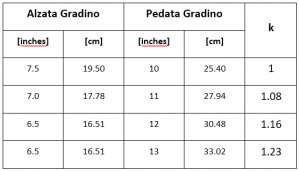
Pathfinder utilizza queste informazioni per determinare i valori di k per qualsiasi scala costruendo una funzione lineare a tratti che mappa i valori della “pendenza” di una scala in k utilizzando questi dati noti.
La pendenza di una scala è definita come: 𝑠𝑡𝑒𝑝 𝑠𝑙𝑜𝑝𝑒 = Alzata del gradino / Pedata del gradino
Per pendenze superiori a 0,75 (il massimo nella tabella 7.5/10), i valori vengono estrapolati fino a un minimo di k di 0,034. Ciò garantisce che scale molto ripide non causino eccessivi rallentamenti agli occupanti. Per pendenze di gradini inferiori a 0,5 (il minimo nella tabella), 𝑘 è linearmente interpolato a 1,4 con una pendenza di 0 (sebbene non sia realistico, ciò corrisponderebbe a una scala piatta). La funzione che descrive la variazione di 𝑘 in funzione della pendenza della scala è riportata nella seguente Figura.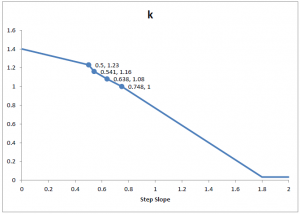
Per modificare le velocità di percorrenza sui pavimenti piani, nelle scale e nelle rampe, L’utente può assegnare dei modificatori di velocità e delle costanti di velocità per simulare gli effetti ambientali come fumo oppure particolari geometrie come scale mobili e rampe mobili. Per impostazione predefinita, tutti i modificatori di velocità sono fissati a 1.
Il modello MassMOTION
MassMotion assegna gli attributi fisici e comportamentali degli agenti con dei valori di default così come indicato nella seguente tabella, dove è indicato i valori minimi e massimi dei singoli attributi per i quali è prevista una distribuzione di probabilità uniforme.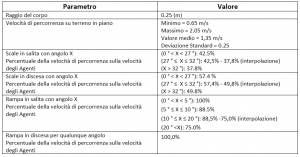
Dati sperimentali
In “Pedestrian and Evacuation Dynamics” di R.D. Peacock, E.D. Kuligowski, J.D. Averill; sono riportati molti esperimenti relativi all’esodo delle di gruppi di persone, in particolare un esperimento è stato condotto su quattro scale con pendenza diversa come da seguente tabella: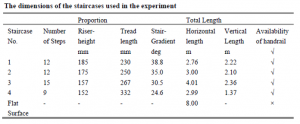
Nell’esperimento, a ogni partecipante è stato chiesto di salire e scendere ogni scala alla sua normale velocità e con velocità di camminata rapida, sono quindi stati realizzati quattro modelli di velocità per ogni partecipante: la normale velocità ascendente, la normale velocità discendente, la velocità di salita veloce e la velocità di discesa rapida. Lo stesso esercizio è stato compiuto per ognuna delle quattro scale. L’esperimento comprendeva due gruppi di partecipanti: uno composto da persone di età pari o superiore a 60 anni, mentre l’altro era composto da studenti universitari e impiegati. Le caratteristiche dei partecipanti sono riportate nella seguente tabella (sono anche state considerate le persone sovrappeso):
I risultati mostrano che quando la velocità di percorrenza su scale degli agenti, sono stimate in funzione della velocità su superfici piane usando un coefficiente di riduzione, la pendenza della scala deve essere presa in considerazione.
I risultati sperimentali sono sintetizzati nella seguente tabella: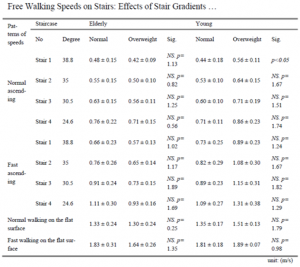
In “Investigation and Simulation on Human Evacuation Behaviour in Large Hospital Building in Shenyang” – Ze-min Jiang, Pei-hong Zhang, Rong-xue Shang, Xiang-liang Tian, è riportata la seguente tabella risultato di osservazioni sperimentali in ospedali: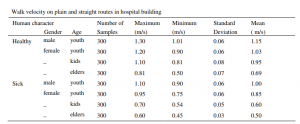
Si può osservare che i pazienti camminano lentamente con una percentuale del 70 ÷ 90% delle persone sane che dicono dello stesso sesso e di età simili. La velocità dei bambini e degli anziani è più lenta rispetto ai giovani. Inoltre si osserva che i pedoni in gruppi sono più comuni negli ospedali, i gruppi sono per lo più di un paio di persone sia in salute che malate; questi tipi di gruppo camminano a 0,7 ÷ 0,9 m/s, che è una velocità relativamente più lenta rispetto a quella delle persone comuni. L’analisi della correlazione è stata effettuata in base a SPSS17.0, i risultati sono stati elencati nella seguente Tabella.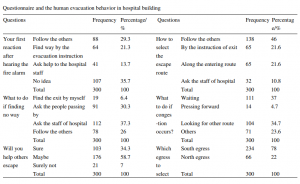
E’ interessante notare che circa 1/3 degli occupanti l’ospedale non hanno alcuna idea sulla prima azione da compiere dopo che si è verificato l’allarme antincendio. Risposte simili ai questionari sono date anche in altre tipologie di edifici pubblici, tuttavia, la percentuale di questa risposta, nel caso dell’ospedale, è molto al di sopra delle risposte simili nei normali edifici pubblici, ciò può essere attribuito allo stato fisico delle persone che hanno risposto al questionario.
Circa 1/3 degli occupanti, dopo avere sentito l’allarme, ha deciso di seguire l’azione di altri. Poco più del 10% degli occupanti ha deciso di chiedere aiuto al personale dell’ospedale. Quasi il 20% degli occupanti ha scelto lo stesso percorso utilizzato entrando, il 20% degli occupanti ha tentato di seguire le indicazioni delle uscite di sicurezza.
Si è visto che se l’occupante non riesce a trovare la via di fuga il 37,3% delle persone ha chiesto aiuto al personale ospedaliero, questo comportamento può essere attribuito alla psicologia caratteristica delle persone che si trovano in ospedale, ne consegue che il personale ospedaliero deve essere formato e addestrato allo specifico scopo, in quanto la capacità di indirizzare e aiutare i pazienti in evacuazione contribuisce in modo notevole alla sicurezza antincendio dell’ospedale.
In “Guide to Human Behavior in Fire 2nd Edition” – SFPE Task Group on Human Behavior in Fire è riportata la seguente tabella di origine sperimentale nella quale sono riportate le velocità di camminamento in funzione dell’esposizione al fumo.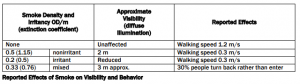
Evacuazione delle grandi aree adibite a pubbliche manifestazioni
La Circolare del Ministero dell’Interno del 18 luglio 2018 – “Modelli organizzativi per garantire alti livelli di sicurezza in occasione di manifestazioni pubbliche. Direttiva.” prevede la suddivisione della zona in settori
Per affollamento fino a 10.000 persone non è richiesta, ai fini di safety, la suddivisione in settori. Per affollamento superiore a 10.000 persone e fino a 20.000 persone, si dovrà prevedere la separazione in almeno due settori. Per affollamento superiore a 20.000 persone si dovrà prevedere la separazione in almeno tre settori. I settori devono essere realizzati secondo i seguenti requisiti:
- i settori dovranno essere separati tra loro mediante l’interposizione di spazi liberi in cui è vietato lo stazionamento di pubblico ed automezzi non in emergenza aventi larghezza non inferiore a 5 metri.
- lungo la delimitazione della suddetta zona di separazione si dovranno prevedere degli attraversamenti presidiati in ragione di uno ogni 10 m.
- le separazioni di tipo “mobile” devono garantire la resistenza ad una pressione su metro lineare superiore a 300 N/m al fine di evitare che, a seguito di ribaltamento, le stesse separazioni possano causare la caduta di persone e il conseguente calpestamento.
- lungo le separazioni di tipo mobile si dovranno prevedere degli attraversamenti presidiati in ragione di uno ogni 10 m
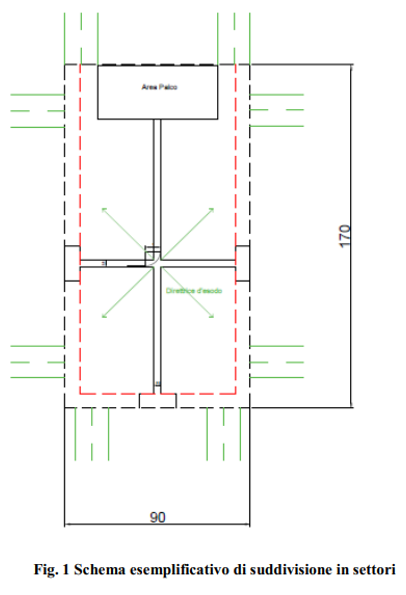
Lo schema esemplificativo riportato nella Figura costituisce un’ipotesi di suddivisione dell’area in settori. Tale soluzione può ritenersi applicabile ove i lati non delimitati da transenne antipanico consentano l’allontanamento del pubblico verso le vie di esodo. L’esigenza di dover delimitare l’intera area interessata dall’evento per esigenze non solo di safety, ma anche di security, potrebbe essere soddisfatta anche interponendo opportuni spazi liberi di idonea superficie, da ricavare lungo il perimetro della zona occupata dal pubblico, ovvero annettendo la viabilità adiacente.
Sono riportate di seguito delle simulazioni relative a P.zza S.Carlo a Torino, con la presenza prevista di 20.000. Le simulazioni sono relative alla spazio suddiviso in settori e non suddiviso in settori.
Simulazione 1
La simulazione di evacuazione prevede l’utilizzo del modello Pathfinder ed è relativa alla realizzazione di un’area per il contenimento di 20.000 persone all’interno della Piazza S. Carlo a Torino. La piazza è dotata di 5 varchi di esodo, completamente liberi, in corrispondenza delle strade (via Vittorio Alfieri, via Giovanni Giolitti, via S. Teresa, via Roma, via Maria Vittoria).
La piazza ha dimensioni 168.0 m x 76.0 m = 12.768 mq.
La densità di affollamento teorica è uguale a 20.000/12.768 = 1.56 per/mq.
Le persone sono distribuite su un’area inferiore di 148.0 m x 68.0 m = 10.064 mq, con una densità di affollamento reale di 20.000 / 10.064 ≈ 2 persone/mq.
Questa semplice simulazione di evacuazione prevede:
- Le 20.000 persone sono distinti per tipo con le seguenti percentuali (10% Anziani – 10% Bambini – 20% Uomini – 20% Donne – 40% Giovani (uomini e donne)), ogni tipologia di agente ha caratteristiche proprie.
- Le vie laterali sono tutte aperte e i relativi percorsi sono liberi.
- I portici lungo la piazza non sono considerati.
- Non è previsto alcun ostacolo ad eccezione del monumento posto al centro della piazza.
- La via Roma fra la Chiesa di S. Cristina e la chiesa di S. Carlo Borromeo e le due vie laterali che adducono a piazza CLN sono bloccate, e quindi non accessibili.
Simulazione 2
La simulazione è del tutto analoga alla Simulazione 1, in questo caso è stato utilizzato il modello FDS+EVAC.
I risultati in termini di tempi di evacuazione sono simili.
Seconda Parte dell’articolo
Nella seconda parte dell’articolo sono riportate delle simulazioni che tengono conto della presenza dei portici lungo il perimetro della piazza e di altri ostacoli all’evacuazione. In questo caso la geometria del dominio di calcolo è meglio definita.
Sono stati esaminati i casi relativi alla piazza suddivisa in settori con ampiezza dei varchi di uscita di 2.40 m e di 1.20 m, e della piazza non suddivisa in settore, inoltre è stato analizzato il comportamento della folla considerando aperti i varchi, che dalle strade laterali alla chiese di S. Carlo Borromeo e di Santa Cristina, adducono a piazza CLN.
 |
 |
 |
 |
La bibliografia riporta tutti i seguenti documenti, per accedere a tutti i documenti utilizzare il seguente link.
N.B. La bibliografia è accessibile agli utenti con accesso a “Tutti i contenuti”.
| Building evacuation: Principles for the analysis of basic structures through dynamic flow networks S. Casadesús-Pursals, F. Garriga-Garzón |
| A Review of Building Evacuation Models Erica D. Kuligowski, Richard D. Peacock – Fire Research Division Building and Fire Research Laboratory – NIST |
| The Process of Verification and Validation of Building Fire Evacuation Models (E. Ronchi, E. D. Kuligowski, P. A. Reneke, R. D. Peacock, D. Nilsson) |
| Social force model for pedestrian dynamics D. Helbing, P. Molnár |
| Simulating of Pedestrian Crowds in Normal and Evacuation Situations D. Helbing, I. Farkas, P. Molnár,T. Vicsek |
| Simulating dynamical features of escape panic D. Helbing, I. Farkas, P. Molnár,T. Vicsek |
| Integration of an Agent Based Evacuation Simulation and the State-of-the-Art Fire Simulation T. Korhonen, S. Hostikka, S. Heliövaara, H. Ehtamo, K. Matikainen |
| FDS+Evac: Modelling Social Interactions in Fire Evacuation T. Korhonen, S. Hostikka, S. Heliövaara, H. Ehtamo |
| FDS+Evac: An Agent Based Fire Evacuation Model T. Korhonen, S. Hostikka, S. Heliövaara, H. Ehtamo |
| Evacuation modelling: Comparison of (FDS + Evac) with Simulex R. van Herpen, J.E. Huls, W. Lam, A. van Zeeburg |
| Study on Applicability of FDS+Evac for Evacuation Modeling in Case of Road Tunnel Fire J. Glasa, L. Valasek |
| Human behavior in road tunnel fires: comparison between egress models (FDS+EVAC, Steps, Pathfinder) E. Ronchi, D. Alvear, N. Berloco, J. Capote, P. Colonna, A. Cuesta |
| Fire Dynamics Simulator with Evacuation: FDS+Evac Technical Reference and User’s Guide Timo Korhonen |
| Guide to Human Behavior in Fire 2nd Edition SFPE Human Behavior in Fire Task Group 1st Draft – Public Comment Version |
| Assessment of Total Evacuation Systems for Tall Buildings Final Report E. Ronchi, D. Nilsson |
| Pedestrian planning and design guide Land Transport New Zealand |
| Safety in Numbers? Modelling Crowds and Designing Control for the Notting Hill Carnival M. Batty, J. Desyllas, E. Duxbury |
| Verification of a pedestrian simulation tool using the NIST recommended test cases M. L. Isenhour, R. Lohner |
| The impact of smoke on walking speed K. Fridolf, K. Andrée, D. Nilsson, H. Frantzich |
| La gestione dell’emergenza a supporto della progettazione Stefano Zanut |
| Computational Models for Human Behavior in Fire Evacuations Simo HeliÄovaara |
| Human behavior under fire situations – portuguese population E. Cordeiro, A. Leça Coelho, R. JF. Rossetti, J.E. Almeida |
| Evacuation experiments in offices and public buildings S. Hostikka, T. Paloposki, T. Rinne, J. Saari,T. Korhonen |
| A Proposal for the Goals and New Techniques of Modelling Pedestrian Evacuation in Fires T. Korhonen, S. Hostikka, O. Keski-Rahkonen |
| Panic and human behaviour in fire R. F. Fahy, G. Proulx, L. Aiman |
| Modeling Human Behavior during Building Fires E. D. Kuligowski |
| The Process of Human Behavior in Fires E. D. Kuligowski |
| Data collection and analysis of evacuation situations T. Rinne, K. Tillander, P. Grönberg |
| Simulating large-scale evacuation scenarios in commercial shopping districts – methodologies and case study M. D. Rossetti, Q. Ni |
| Egress Design Solutions: A Guide to Evacuation and Crowd Management Planning J. Tubbs, B. Meacham |
| Collection of Evacuation Data for Large Passenger Vessels at Sea E.R. Galea, R.C. Brown, L. Filippidis, and S. Deere |
| Design Fires for Means of Egress in Office Buildings based on Full-scale Fire Experiments S. KAKEGAWA, Y. YASHIRO, H. SATOH, H. KURIOKA, I. KASAHARA, Y. IKEHATA, N. SAITO, T. TURUDA |
| Computational study of social interactions and collective behavior during human emergency egress J. Fang |
| Analysing the human behavior in a fire drill. comparison between two evacuation software: FDS+EVAC and Pathfinder Z. C. GRIGORAŞ |
| Analysis of Published Accounts of the World Trade Center Evacuation Rita F. Fahy, Guylène Proulx |